jaecall.blogg.se - Standard normal table definition

#STANDARD NORMAL TABLE DEFINITION FULL#

The height of individuals in a large group follows a normal distribution pattern.

#STANDARD NORMAL TABLE DEFINITION FULL#

The full normal distribution table, with precision up to 5 decimal point for probability values (including those for negative values), can be found here. Then check for the first 2 significant digits (0.2) in the rows and for the least significant digit (remaining 0.04) in the column. To find the probability related to z-value of 0.239865, first round it off to 2 decimal places (i.e. A snap-shot of standard z-value table containing probability values is as follows: Z = (X – mean)/stddev, where X is the random variable.īasically, this conversion forces the mean and stddev to be standardized to 0 and 1 respectively, which enables a standard defined set of Z-values (from the Normal Distribution Table) to be used for easy calculations. To facilitate a uniform standard method for easy calculations and applicability to real-world problems, the standard conversion to Z-values was introduced, which form the part of the Normal Distribution Table. Plotting and calculating the area is not always convenient, as different datasets will have different mean and stddev values. Where X is a value of interest (examples below). probability of data values between 65 and 85 probability of data values being greater than 95 probability of data values being less than 70

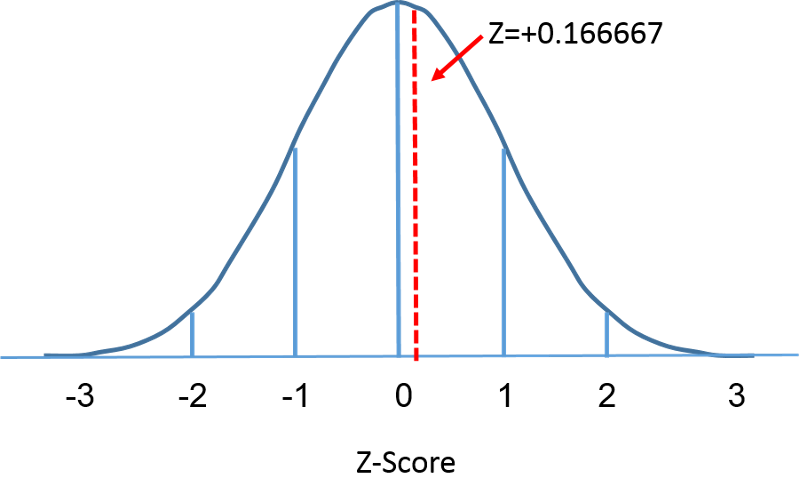
The area under the bell-shaped curve, when measured, indicates the desired probability of a given range:

99.7% of data values are within 3 standard deviations of the mean (-3 to +3).

95.4% of data values are within 2 standard deviations of the mean (-2 to +2).

68.3% of data values are within 1 standard deviation of the mean (-1 to +1).

The distribution is completely described by its mean and stddevĪs can be seen from the above graph, stddev represents the following:.

The total area under the curve is equal to 1 for mean=0 and stdev=1.

The mean is at the middle and divides the area into two halves.

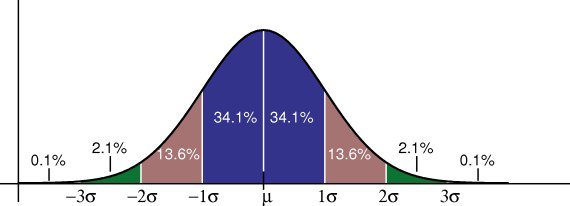
The normal curve is symmetrical about the mean.For any normally distributed dataset, plotting graph with stddev on horizontal axis, and number of data values on vertical axis, the following graph is obtained. For a normal distribution, the data values are symmetrically distributed on either side of the mean. The stddev value has a few significant and useful characteristics which are extremely helpful in data analysis. Since DataSet1 has all values same (as 10 each) and no variations, the stddev value is zero, and hence no pink arrows are applicable.

This is represented by standard deviation value of 2.83 in case of DataSet2. The pink arrows in the second graph indicate the spread or variation of data values from the mean value. The red horizontal line in both the above graphs indicates the “mean” or average value of each dataset (10 in both cases). Image by Sabrina Jiang © Investopedia 2020

Dataset 1 = įor Dataset1, mean = 10 and standard deviation (stddev) = 0įor Dataset2, mean = 10 and standard deviation (stddev) = 2.83.

Normal distribution tables are used in securities trading to help identify uptrends or downtrends, support or resistance levels, and other technical indicators.

Properties of a normal distribution include: the normal curve is symmetrical about the mean the mean is at the middle and divides the area into halves the total area under the curve is equal to 1 for mean=0 and stdev=1 and the distribution is completely described by its mean and stddev.

To facilitate a uniform standard method for easy calculations and applicability to real-world problems, the standard conversion to Z-values was introduced, which form the part of the Normal Distribution Table.

The normal distribution formula is based on two simple parameters-mean and standard deviation-that quantify the characteristics of a given dataset.